DE SITV EIVS, QVO AD MVNDI DIAMETRVM, ET DISTANTIA A TERRA CENTRO VNIUERSI.

ARDUUM est, subtilique indiget ingenio, stellarum a nobis indagare remotionem, propter incredibilem earum a terra distantiam: nec vlla ratione commodius et certius id prestari potest, quam per paralaxeos, si quam habent, mensuram. Si enim stella aliqua horizonti vicina, alio in loco cernatur, quam vbi altissima vertici appropinquat, necessarium est eam reperirj in aliquo orbe, respectu cuius terra sensibilem habeat magnitudinem. Quam vero longe remoueatur dictus orbis, paralaxeos quantitas semidiametro terræ collata, manifestabit. Sin vero stella tam iuxta horizontem, quam verticem, in eodem N primi mobilis puncto cernaturA, non dubium est, eam, vel in octaua Sphæra, vel non longe infra, in orbe, cuius respectu tota terra punctj vicem gerat, locum obtinere. Vt C1v|igitur nobis ea ratione innotesceret, vtrum hæc stella in Elementari regione, autA inter cœlestes orbes existeret, qualemque ab ipsa terra haberet distantiam, indagauimus anA vllam, et quantam, haberet paralaxin, idque hoc modo. Interuallum inter hancA et Schedir Cassiopeiæ (eo quod hæc stella fere cum noua, Meridianum vnâ obtineat) obseruaui cum verticj proxima esset, 6 tantum gradibusA ab ipso zenit remota (ideoque nullam, etiam terræ propinqua in eo loco induceret paralaxin, sed locus eius visus et verus in vnum punctum propter fereA coincidentes a terræ centro et superficie lineas, vnitur). Idem præstiti cum longissime a zenit remota, Horizonti proxima esset: et vtrobique eandem præcise a dicta fixa inuenj distantiam nullo minuto variatam, partium videlicet 7 et 55 Minutorum. Idemque per alias stellas multiplicj facta obseruatione expertus sum: vnde hanc nouam stellamA nullam habere aspectus diuersitatem, etiam Horizontj vicinam, concludo. Alias enim in minima sua altitudine longius remota fuisset I.25|a prænominata stella in pectore Cassiopeæ, quam in altitudineA maxima. QuapropterA non in Elementarj regione infra Lunam, sed longe supra, in orbe, cuius respectu terra sensibilem non obtineat magnitudinem, collocarj hanc stellam necessarium eritA. Si enim in suprema æris regione infra concauam sphæræ Lunaris regionem esset, sensibilem induxisset in circulo altitudinis variationem, horizontj proxima, ab eo loco quem obtinebat verticj vicina. DeC2r|scribatur enim certioris demonstrationis causa, circulus repræsentans Meridianum, vel aliquem alium verticalem primi mobilis, in quo loca omnium stellarum consideranturA, qui sit CBDE, cuius centrum sit A: Diameter vero BE verticem, CD Horizontem designet: sit insuperA eodem centro descriptus circulus MKL, qui terrenj orbis circumferentiam denotet. Inter hos alius signetur circulus GHFI, qui infimum sphæræ Lunæ et terræ proximum repræsentet ambitum, in quo stellam hanc existere fingamus: sitque primum in maxima sua altitudine iuxta punctum G: Manifestum est quod careat omni diuersitate aspectus. Ambæ enim lineæ a centro terræ, et oculo in eius superficie constituto eductæ, in vnum eundemque primi mobilis circuli, videlicet CBDE cadent locum, in punctum videlicet B, vel prope, si stella non sit præcise in G. Hæc enim 6 gradibus a vertice remouetur, cum nobis altissima sit, qui tamen nullam sensibilemA inducunt variationem ab ipso vertice. Constituatur vero hæc stella in eodem circulo GHFI, in minima sua altitudine, idque in puncto O, necessarium erit eam in alio loco extremj circulj videri, si oculus constituatur in K superficie terræA, quam si in A eiusdem centro. Ductis enim lineis a K superficie, et a centro terræ A, per O locum stellæ, in extremum orbem BDEC cadet linea ab A per O in P: a K vero per idem O in Q. Est igitur PQ, arcus primi mobilis, stellæ aspectus diuersitatem ostendens.

Figur 3 

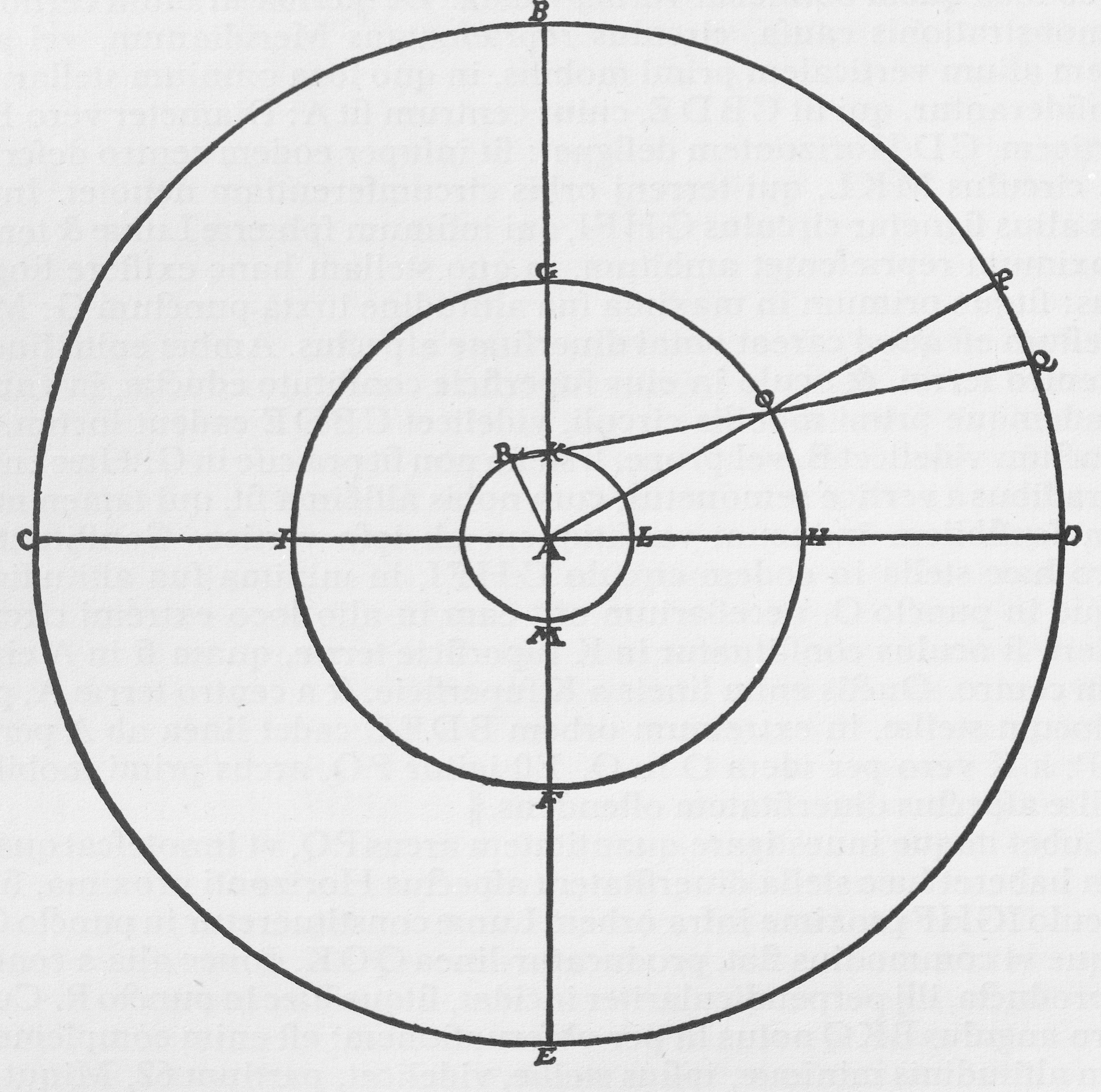
C2v|Lubet itaqueA inuestigare quantitatem arcus PQ, vt innotescat quantam haberetA hæc stella diuersitatem aspectus Horizonti proxima, si in circulo IGHF proxime infra orbem Lunæ constitueretur in puncto O. C3r|Idque vt commodius fiat, producatur linea QOK, donec alia a centro A productaA, illj perpendiculariter incidat, sitque hæcA in puncto R. Cum veroA angulus BKQ notus sit per obseruationem: est enim complementum altitudinis minimæ, ipsius stellæ, videlicet, partium 62, Minut. 5A, non ignorabitur ei contrapositus RKA ipsi æqualis. Est insuper angulus KRA ex hypothesiA rectus: et latus KA notum est per mensuram quamcumque: est enim semidiameterA ipsius terræ: non ignorabiturA AR, per 29 propositionem Regiomontanj de triangulis planis. Si itaque ponatur semidiameter terræ KA, partium 100000, tanquam N sinus totus, cum sit latus recto angulo, qui ad R, oppositum, euadit latus A R, partium 88363. Nunc demum concipio triangulum ROA, cuius duo I.26|latera RA, et AO, nota sunt. Est enim AO distantia a centro terræ ad infimam superficiem orbis Lunæ, quam vnâ cum Copernico statuimus partium 5200000, qualium semidiameter terræ AK, erat 100000 (lubet enim maioribus numeris negocium hoc absoluere, vt calculus eo fit commodior et exactius innotescat) cumque in dicto triangulo angulus ORA ex hypothesi rectus fit, per 27 propositionem Regiomontanj de triangulis planis, non latebit angulus ROA. Multiplicato enim latere AR in totum sinum, producuntur 8836300000, qui numerus per latus AO diuisus, relinquit 1699 partes, sinum videlicet angulj ROA, cuius arcus est 0 partium, 58½ C3v|Minutorum, qui numerus anguli quæsitj determinat quantitatem. Huic vero angulo ROA, æqualis est angulus POQ : est enim illj contrapositus, vt patet N ex elementis Geometriæ. Idcirco arcus PQ, qui hunc angulum metitur (nam propter immensam I.27|distantiam inter Sphæram Lunæ et primum mobile, arcus PQ non differt sensibiliter ab arcu circulj interuallo OP ijsdem lineis intercepto) stellæque designat paralaxin, eritA minutorum 58½, quod erat quærendum. Tantam igitur habuisset hæc stella in O posita, aspectus diuersitatem, ab eo loco, quem prope verticem obtinebat, in eum vbi Horizontj proxima conspiciebaturconspiciebaturA. Id autem per multas et diligentes obseruationes (vt supra dixi) factas, exquisito et minime fallaci instrumento, falsum inuenimus. Vnde concludo hanc nuper visam stellam non esse in circulo IGHF, suprema videlicet aërisA regione, proxime infra Lunæ orbemA, nec in aliquo loco adhuc terræ propiore. Tunc enim maiorem induxisset quantitatem arcus PQ, maiorque fieret aspectus diuersitas: sed longe supra sphæram LunæA, in ipso cœlo locum obtinere, idque in orbe aliquo, tanto interuallo a terra remoto, vt linea KA semidiameter terræ, non habeat respectu eius sensibilem quantitatem: sed tota terra illj collata nil præter puncti vicem habere animaduertatur, idque in octaua sphæra, vel non longe ab hac in altioribus trium superiorum Planetarum orbibus fierj, ab artificibus compertum est. Vnde hæc stella in ipso cœlo, vel in octauo orbe cum C4r| reliquis fixis, vel in proxime huic subiectis sphæris constituetur. Quod autem nec in orbe Saturnj, nec Iouis, Martisue, aut aliorum Planetarum existat, hinc patet, quod elapso iam sexA mensium spacio, nullo minuto ab eo loco, in quo primum eam conspeximus, motu proprio progressa estA, quod fieri oportebat si in aliquo Planetarum orbe esset. Moueretur enim motu ipsius orbis peculiari, contra primi mobilis rationemA, nisi in altero polorum, orbium secundi mobilis quiesceret, a quo tamen 28A partibus, vt supra ostendiA, remouetur. Toti enim orbes proprijs polis reuoluti, sua circumducunt sidera, vel ab illis, N (vt Plinio et quibusdam alijs placere video) circumaguntur. Nisi quis receptam a Philosophis et Mathematicis sententiam negare velit, solasque stellas immotis orbibus conuolui (quod absurdum est) asserere. Vnde si hæc stella in aliquo orbium septem errantium siderum constitueretur, necessario cum ipso orbe, cui affixa esset, contra diurnam reuolutionem circumduceretur.A Atque hic motus etiam in lentissimo Saturni orbisA progressu tanto temporis interuallo, etiam absque omni instrumento intuentiA animaduerteretur. Quapropter hæc stella noua nec in Elementari regione infra Lunam, nec in orbibus septem errantium siderum, sed in octaua sphæra inter reliquas fixas locum habet, quod erat demonstrandum. Hinc sequitur illam non esse aliquam peculiarem Cometarum speciem, nec quoduis aliud apparens igneum Metheoron. Hæc enim omnia non in ipso cœlo generantur, sed infra C4v|Lunam in superiori aëris regione existunt, vt omnes testantur Philosophi: nisiA quis cum N AlbategnioA statuere velit, Cometas, non in aëre, sed inA cœlo nascj. Ille enim se I.28|Cometam supra Lunam in sphæra Veneris obseruasse existimat: quod an fierj possit, nobis nondum constat: Sed Deo dante aliquando, si nostra ætate aliquis extiterit Cometa, eius rej certitudinem inquiremus. Hoc etsi verum esse ponamus (quod vnâ cum omnibusA Philosophis vix admitto) tamen non sequitur hanc stellam Cometarum esse speciem: tum propter ipsam formam, quam habet cum veris stellis communem, et ab omnium hactenus visorum Cometarum figura dissimilem: tumA quod nullo motu proprio, tanto tempore, vel in latitudinem, vel in longitudinem processit, vt in Cometis fierj animaduersum est. Licet enim hiA aliquando in vno loco per aliquot dies quiescere videantur: tamen non ita diu, nec ita exacte, diligenter per instrumenta exquisita obseruatione facta, eundem seruant positum.A Concludo igitur hanc stellam, non esse vllam Cometarum speciem, vel aliquod igneum metheoron, siue infra Lunam, siue supra generentur: sed lucentemA in ipso firmamento esse stellam, nulla ætate a mundj exordio ante nostra tempora prius conspectam. Atque hæc de stellæ eius situ, tum quo ad zodiacum, tum quo ad mundj diametrum, et cœlj orbes, sufficienter dicta demonstrataqueA existimo: nunc ad reliqua progrediar.

Om dens position i forhold til verdens diameter og dens afstand fra Jorden, verdens centrum.

Det er vanskeligt og kræver et meget skarpt intellekt at undersøge stjernernes afstand fra os på grund af deres utrolige afstand fra Jorden. Det kan ikke gøres på nogen lettere og mere sikker måde end ved en måling af deres parallakse, hvis de har en sådan. Hvis nemlig en stjerne nær horisonten ses på et andet sted, end hvor den på sit højeste nærmer sig zenit, må den nødvendigvis findes i en af kredsene, i forhold til hvilken Jorden har en mærkbar størrelse. Hvor langt den omtalte kreds er væk, vil parallaksens størrelse sammenholdt med Jordens halvdiameter vise. Hvis stjernen både nær ved horisonten og ved zenit ses i det samme punkt af Nden første bevægede kreds, er der ingen tvivl om, at den enten har sin plads i den ottende sfære eller ikke langt derunder, i en kreds i forhold til hvilken Jorden er som et punkt. For at det nu C1v|således kunne stå os klart, om denne stjerne opstod i elementarregionen eller blandt de himmelske kredse, og hvilken afstand den havde fra selve Jorden, undersøgte vi på følgende måde, om den overhovedet havde nogen parallakse, og i givet fald hvor stor: Jeg observerede afstanden mellem den nye stjerne og Schedir i Cassiopeia (denne stjerne har nemlig næsten den samme meridian som den nye), når den var nærmest zenit; den var kun 6 grader væk fra selve zenit (og derfor kunne den ikke lave nogen parallakse på dette sted, selvom den var nær ved Jorden, men både dens tilsyneladende og sande position forenes i ét punkt på grund af de næsten sammenfaldende linjer fra Jordens centrum og overflade). Det samme udførte jeg, da den var længst væk fra zenit og nærmest horisonten, og begge steder fandt jeg nøjagtig den samme afvigelse fra den omtalte fiksstjerne på 0 minutter, nemlig 7 grader og 55 minutter. Jeg konstaterede det samme ved mange gange gentagne observationer af andre fiksstjerner. Deraf slutter jeg, at denne nye stjerne ikke har nogen forandring i sin synsvinkel, selv når den er nær horisonten. Ellers ville den nemlig have fjernet sig mere I.25|fra den føromtalte stjerne i Cassiopeias bryst i sin mindste højde end i sin største højde. Derfor må man nødvendigvis placere denne stjerne ikke i elementarregionen neden for Månen, men langt ovenover i en kreds, i forhold til hvilken Jorden ikke har en mærkbar størrelse. Hvis den nemlig havde været i den øverste del af luftregionen, altså neden for månesfærens konkave region, ville den have forårsaget en mærkbar variation i højdecirklen, når den var nærmest ved horisonten, i forhold til det sted, hvor den er C2r|nær zenit. Lad der (af hensyn til et mere klart bevis) være tegnet en cirkel, som gengiver meridianen eller en anden vertikal i den første bevægelige kreds, hvor alle stjerners positioner ses. Lad diameteren BE betegne vertikalen, CD horisonten. Lad der desuden være beskrevet en cirkel med samme centrum MKL, som angiver Jordens omkreds. Mellem disse skal der også angives en anden cirkel GHFI, som gengiver månesfærens nederste løb nærmest ved Jorden, hvor vi skal forestille os, at denne stjerne befinder sig. Lad den nu være i sin største højde ved punktet G. Det er klart, at den mangler enhver form for ændring i synsvinkel. Begge linjer er nemlig trukket fra Jordens centrum og fra et øje på dens overflade til ét og samme punkt på den øverste bevægelige kreds, dvs. CBDE, og vil ramme det samme sted, nemlig i punkt B eller nærved, hvis stjernen ikke præcis er i G. Dette punkt flytter sig nemlig 6 grader fra zenit, når den står højest for os, men den udgør ikke nogen mærkbar forskel fra zenit. Lad nu denne stjerne befinde sig i den samme cirkel GHFI i sin mindste højde, dvs. i punktet O. Den må nu nødvendigvis ses på et andet sted i den yderste cirkel, hvis øjet befinder sig i K på Jordens overflade, end hvis det var i A ved dens centrum. For hvis linjerne er trukket fra overfladen K og Jordens centrum A gennem stjernens position O til den yderste kreds BDEC, vil linjen falde fra A gennem O til P. Fra K ligeledes gennem O til Q. Derfor er PQ en bue på den første bevægelige kreds og viser stjernens ændring i synsvinkel.

Figur 3 

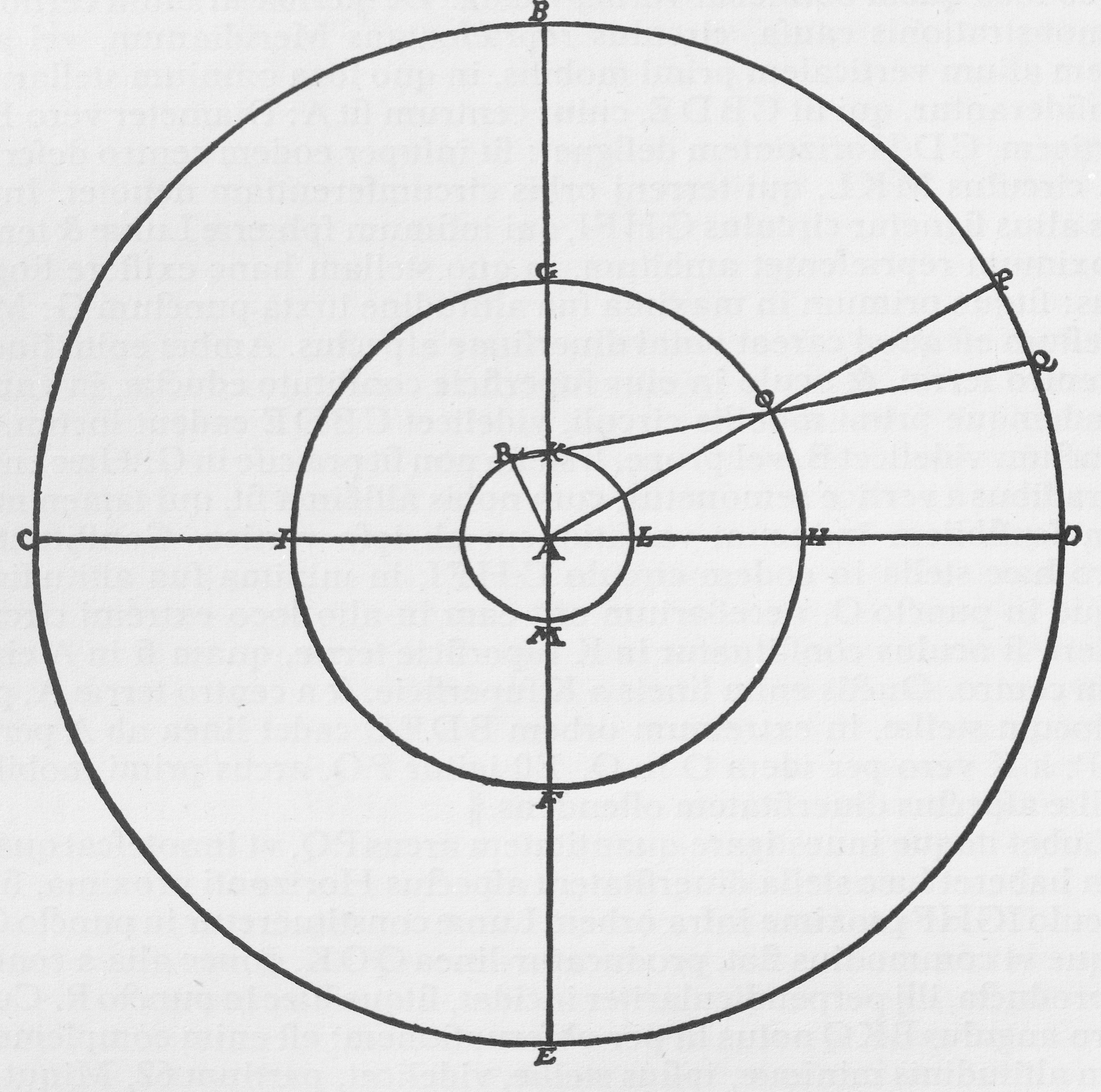
C2v|Vi skal nu undersøge størrelsen af buen PQ for at det kan stå klart hvilken ændring i synsvinklen denne stjerne har nærmest ved horisonten, hvis den befinder sig i punkt O på cirklen IGHF C3r|lige neden for Månens kreds. Lad der, for at det kan ske så let som muligt, være trukket en linje QOK, indtil en anden linje trukket fra centrum A skærer den vinkelret, og lad det ske i punktet R. Da nu vinklen BKQ er kendt ved observation (den er nemlig komplementet til denne stjernes mindste højde, dvs. 62 grader og 5 minutter), så vil dens topvinkel RKA, som er lig med den, også være kendt. Desuden er vinkel KRA if. antagelsen ret, og siden KA er kendt fra enhver måling, den er nemlig Jordens halvdiameter. AR vil være kendt gennem den 29. sætning i Regiomontanus’ bog Om plane trekanter. Hvis altså Jordens halvdiameter KA sættes til 100.000 dele, ligesom Nhele sinus, vil siden AR være på 88.363, eftersom den er siden i en ret vinkel, som står over for R. Nu undersøger jeg først trekanten ROA, hvis to I.26|sider RA og AO er kendt. AO er nemlig afstanden mellem Jordens centrum og den nederste overflade af Månens kreds, som vi i overensstemmelse med Kopernikus har fastsat til 5.200.000 af de dele, hvoraf Jordens halvdiameter AK udgjorde 100.000. (Det er nemlig en fordel at løse denne opgave med store tal, så udregningen bliver nemmere og fremstår mere eksakt). Da vinkel ORA i den omtalte trekant if. antagelsen er ret, vil vinkel ROA fremgå ved den 27. sætning i Regiomontanus’ Om plane trekanter. Hvis siden AR multipliceres med hele sinus, giver det nemlig 8.836.300.000, og divideret med siden AO giver dette tal 1.699 dele, dvs. sinus til vinklen ROA, hvis bue er 0 grader og 58 ½ minutter. C3v|Dette tal angiver den søgte vinkels størrelse. Men vinkel POQ er lig med denne vinkel ROA. Den er nemlig dens topvinkel, som det fremgår af Ngeometriens elementer. Derfor vil buen PQ, som måler denne vinkel og angiver stjernens parallakse, være på 58 ½ minutter, hvilket skulle findes (for på grund af den umådelige I.27|afstand mellem Månens sfære og den første bevægelige kreds afviger buen PQ ikke mærkbart fra cirkelbuen i afstanden OP mellem de samme linjer). Hvis denne stjerne havde befundet sig i punktet O, ville den altså have haft en så stor forandring i synsvinkel fra den position, som den havde nær zenit, til positionen, hvor den blev observeret nær horisonten. Dette har vi imidlertid som sagt vist er forkert ud fra mange og omhyggelige observationer foretaget med et udsøgt og meget lidt fejlbehæftet instrument. Derfor slutter jeg, at denne nyligt sete stjerne ikke er i cirkel IGHF, dvs. i den øvre luftregion, lige neden under Månens kreds, og heller ikke i nogen position endnu nærmere Jorden. I så fald ville den nemlig have forårsaget en større bue PQ, og ændringen i synsvinklen ville have været større. Jeg slutter, at den tværtimod har en position meget højere oppe end Månens sfære, nemlig i selve himlen, tilmed i en kreds, der er så langt væk fra Jorden, at linjen KA (Jordens halvdiameter) ikke har nogen mærkbar størrelse i forhold til den. Hele Jorden skal betragtes som værende blot et punkt sammenlignet med denne afstand, og astronomerne har fundet ud af, at dette sker i den ottende sfære eller ikke langt fra den i de tre øverste planeters kredse. Derfor må denne stjerne placeres i selve himlen, enten i den ottende kreds sammen med C4r|de øvrige fiksstjerner eller i de nærmest underliggende sfærer. At den ikke befinder sig i Saturns, Jupiters, Mars’ eller de andre planeters kredse, fremgår af, at den i de forløbne seks måneder ikke med en egenbevægelse har flyttet sig ét minut fra det sted, hvor vi først observerede den. Dette burde være sket, hvis den havde været i en af planetkredsene. Så ville den nemlig bevæges med den for hver kreds særlige bevægelse imod den første bevægelige kreds’ orden, medmindre den havde stået stille ved den anden af polerne i den anden bevægelige kreds. Den har dog, som jeg ovenfor har vist, en afstand på 28 grader herfra. Alle kredse drejer nemlig om deres egne poler og fører deres egne himmellegemer rundt, eller føres rundt af andre N(som jeg ser, at Plinius og visse andre mener); medmindre man vil benægte filosoffernes og matematikernes overleverede opfattelse og påstå, at kun stjernerne roterer på ubevægelige kredse (hvilket er absurd). Hvis denne stjerne befandt sig i en af de syv vandrende himmellegemers kredse, måtte den derfor nødvendigvis bevæge sig rundt sammen med den kreds, som den var fæstnet på, og mod den daglige omdrejning. Men denne bevægelse ville kunne observeres selv i den langsomste progression i Saturnkredsen i et så langt tidsrum og selv af en, som betragtede den uden brug af instrument. Derfor har denne nye stjerne hverken sin plads i elementarregionen neden for Månen eller i de syv vandrende himmellegemers kredse, men i den ottende sfære blandt de øvrige fiksstjerner. Hvilket skulle bevises.

Heraf følger, at den ikke er en særlig form for komet eller et eller andet tilsyneladende ildmeteor. For alle disse ting opstår ikke i selve himlen, men C4v|neden for Månen i den højere luftregion, som alle filosoffer bekræfter; medmindre man med NAlbategnius vil påstå, at kometer ikke opstår i luften men i himlen. Han mener at I.28|have observeret en komet over Månen i Venus’ sfære. Om det kan forekomme, ved vi endnu ikke, men med Guds hjælp vil vi undersøge rigtigheden af denne sag, hvis der engang i vor levetid skulle komme en komet. Selvom vi antager, at det er sandt (hvilket jeg i overensstemmelse med alle filosoffer næppe kan medgive), følger der ikke heraf, at denne stjerne er en slags komet, dels på grund af formen, som den har tilfælles med de rigtige stjerner, og som er anderledes end alle de hidtil observerede kometers udseende, dels fordi den ikke har bevæget sig fremad med egen bevægelse i hele dette tidsrum, hverken i bredde eller i længde, sådan som det er velkendt, at kometer gør. Det kan godt være, at disse sommetider standser i nogle dage på ét sted, men de holder ikke deres plads så længe og ikke så nøjagtigt, hvilket omhyggelig observation med nøjagtige instrumenter påviser. Jeg slutter derfor, at denne stjerne ikke er en slags komet eller noget andet ildmeteor, hvad enten de opstår under eller over Månen, men at det er en lysende stjerne på selve firmamentet, som ikke har kunnet ses i nogen tidsalder fra verdens skabelse til vore dage. Jeg mener nu, at der er sagt og bevist tilstrækkeligt om denne stjernes position, både hvor den er i forhold til Dyrekredsen, til verdens diameter og himlens kredse. Jeg vil derfor gå videre til det øvrige.