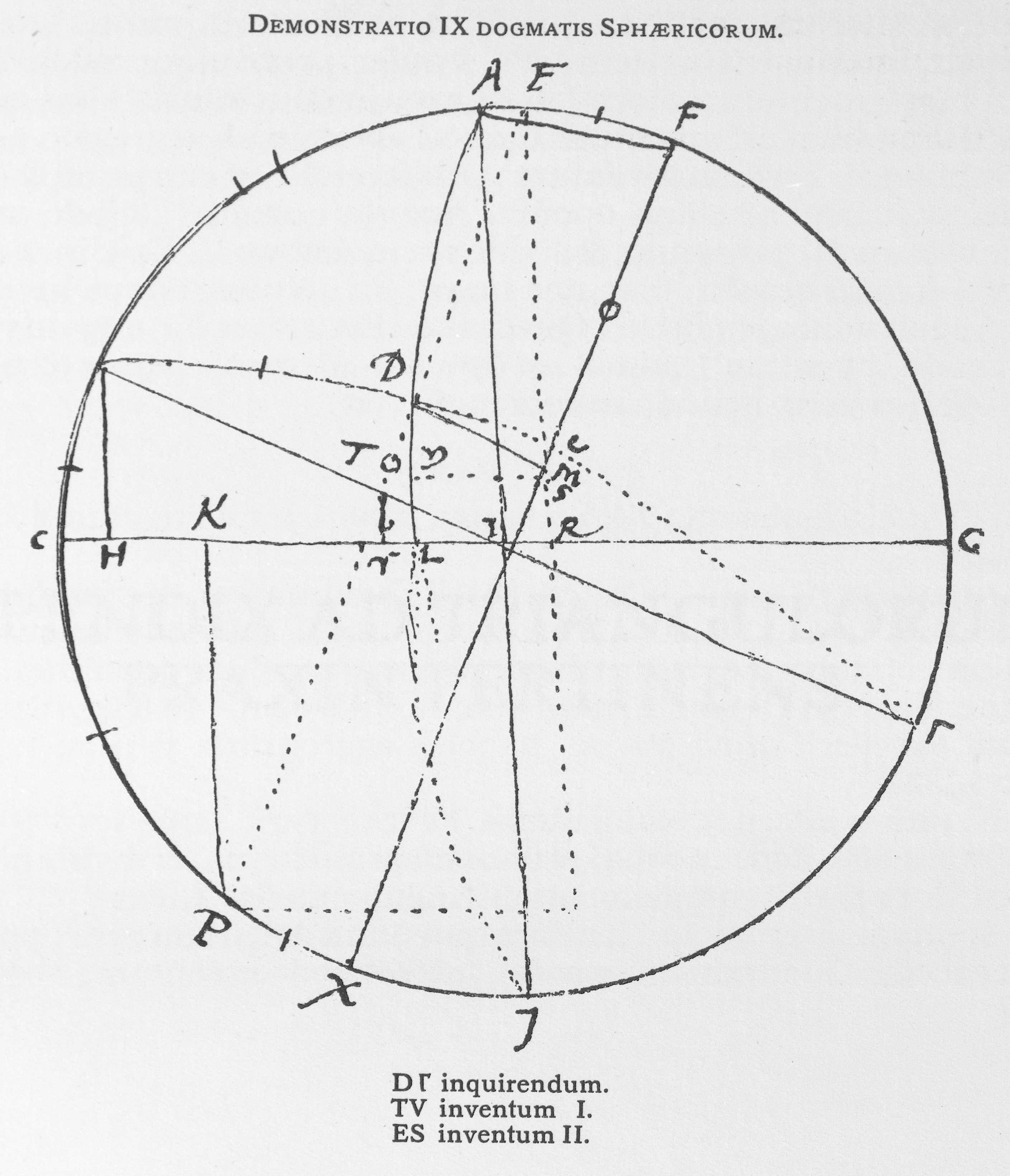
|SEQUITUR DE TRIANGULIS SPHÆRICIS COMPENDIUM CONTINENS DOGMATA NOVEM.
|DOGMA I SPHÆRICORUM.
Trianguli Retanguli, datis duobus lateribus, tertium Recto positum invenire.
Operatio] Minus latus, et complementum maioris invicem adde, et aufer, utriusque residui sinum adde, si complementum maioris lateris maius fuerit minore, alias subtrahe, et differentiæ cape dimidium, et habebis sinum complementi lateris reliqui inquirendi.
|DOGMA II SPHÆRICORUM.
Trianguli Rectanguli, datis duobus lateribus, angulum quemcunque invenire.
Si latus rectum subtendens Angulum cum latere, quod opponitur Angulo inquirendo, data non fuerint, latus, quod ex his ignoratur, primum, per antecedentem operationem inquirendum erit, et hinc procedendum in hunc modum. Multiplica sinum lateris oppositi angulo quæsito per sinum totum, et productum divide per sinum lateris, rectum angulum subtendentis: provenit sinus Anguli inquirendi, cuius arcus illius Anguli quantitatem metitur.
|DOGMA III SPHÆRICORUM.
Trianguli Rectanguli dato uno Angulo, cum Latere adiacente, reliquum Angulum, lateri dato oppositum invenire.
Operatio] Minus datum, et complementum maioris invicem adde, et aufer, utriusque residui sinus subtrahe, vel adde, si Angulus fuerit |maior latere adiacente, residui cape dimidium pro sinu complementi anguli quæsiti, vel sinus lateris oppositi angulo dato, quando angulus est maior latere adiacente.
NB. Habet locum, quando latus adiacens angulo recto fuerit datum: et notandum, quod, quam diu latus datum est minus Angulo dato, debent ambo addi, et auferri, et residuorum sinus coniungi, et dimidiari pro sinu complementi anguli quæsiti; quando vero latus est maius Angulo, potes uti, prout est in exemplo adscripto, per subtractionem sinuum, accipiendo ipsa data, non complementum maioris. Si vero utraque data Quadrantem excesserint, tunc operare per |complementum utriusque dati, subtrahendo invicem sinus aggregati, et differentiæ, quorum et dimidiando est sinus complementj Anguli quæsiti.
|DOGMA IV SPHÆRICORUM.
Trianguli Rectanguli, dato uno angulo, et quovis latere, reliqua invenire.
I. Si latus datum Angulo non recto dato opponatur, multiplica sinum ipsius lateris per totum, et per sinum Anguli dati divide: exit sinus lateris rectum subtendentis. Reliquum latus dabit Dogma I, Angulos vero Dogma II.
II. Si latus datum Recto opponitur Angulo, sinum eius per sinum anguli dati multiplica, et productum divide per totum: exit sinus lateris oppositi Angulo dato. Reliqua inquire per primum et secundum dogma, uti prius.
Si angulus Rectus, et angulus datus lateri dato insideant, operare per antecedentem pro reliquo Angulo: per sequentem vero pro reliquis lateribus.
|DOGMA V SPHÆRICORUM.
Trianguli Rectanguli, datis duobus reliquis Angulis, latus quodcunque invenire.
Multiplica sinum complementi Anguli non recti, subtendentis sive oppositi, lateri quæsito per totum, et productum divide per sinum reliqui Anguli non recti: exit sinus complementi lateris quæsiti.
Pro reliquis autem lateribus multiplica sinum lateris modo inventi per sinum Anguli, respicientis reliquum latus quæsitum, sive rectus fuerit is angulus sive non, productum divide per sinum Anguli, quem subtendit latus nuper inventum: exibit sinus lateris inquirendi. Tertium latus dabit I dogma.
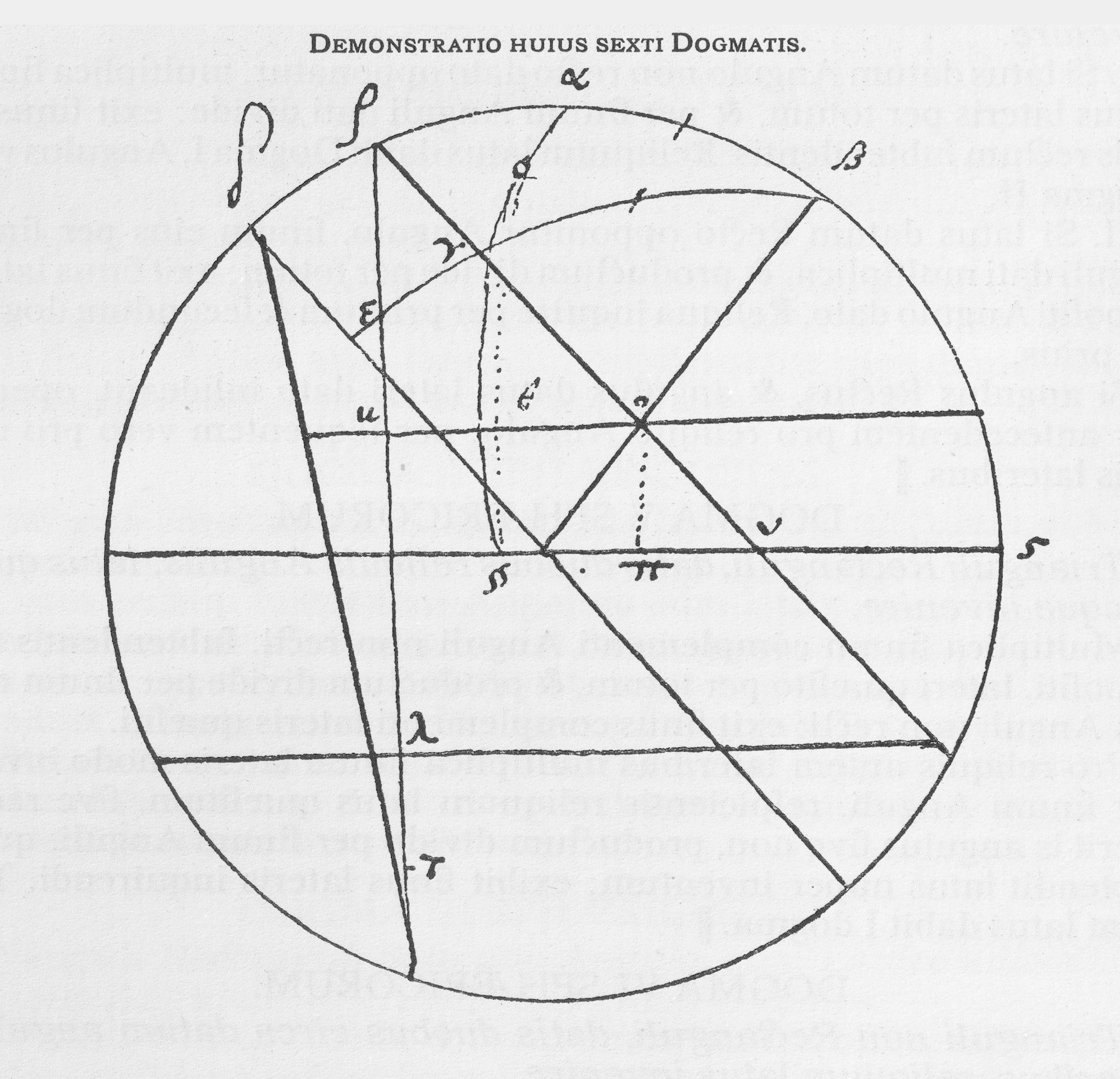
|DOGMA VI SPHÆRICORUM.
Trianguli non Rectanguli, datis duobus circa datum angulum lateribus, reliquum latus invenire.
|Minus latus, et complementum maioris invicem adde, et aufer; utriusque residui sinus invicem adde, si supplementum maioris lateris maius fuerit latere minore; alias aufer, ubi eo minus fuerit; residui dimidium erit inventum I, quod ablatum ab aggregato primo dabit inventum II, per quod multiplica sinum complementi Anguli dati, si acutus fuerit (vel sinum excessus eius Anguli ultra quadrantem, si obtusus), et divide per totum: habebis inventum III. Hoc adde ad inventum I, si angulus datus acutus fuerit, vel subtrahe ab invento I, si obtusus: habebis sinum complementi lateris quæsiti.
VARII CASUS OBSERVATI HUIUS DOGMATIS.
I. Si unum laterum ambientium Angulum datum maius Quadrante fuerit, resultat latus oppositum minus quadrante. Si productum in multiplicatione maius fuerit invento primo: |subducto II multiplicato ab hoc invento I, relinquitur sinus complementi lateris quæsiti.
|DOGMA VII SPHÆRICORUM.
Trianguli non Rectanguli, datis duobus Angulis circa datum latus, Angulum reliquum invenire.
Angulum minorem, et complementum maioris invicem adde, et aufer, residui utriusque sinus adde, si complementum maioris Anguli superet Angulum minorem, vel aufer, si eo minus fuerit, et habebis inventum I, quod aufer â primo aggregato: habebis inventum II, per quod multiplica sinum complementi lateris dati, et divide per totum: exit inventum III, quod adde ad inventum I, si latus datum minus quadrante fuerit; vel subtrahe ab eodem, si maius extiterit: habes sinum complementi Anguli quæsiti. Fuit itaque operatio similis priori
|DOGMA VIII SPHÆRICORUM.
Trianguli non Rectanguli, datis duobus Angulis cum latere alteri eorum opposito, reliqua latera, et Angulum invenire.
Hîc opus erit resolvere Triangulum in duos Rectangulos, ducta perpendiculari ab Angulo ignoto, sive cadat extra, sive intra Triangulum, et deinde operari per III et IV. Exempli gratiâ. Sit Triangulus ABC, cuius Anguli ad A et B sint noti, cum latere AC. Volo inquirere latus BA. Duco itaque perpendicularem ab Angulo C ignoto in BA, quæ sit CD. Trianguli itaque CAD rectanguli datur Angulus ad A cum latere adiacente AC. Ergo per Tertium dabitur AD.
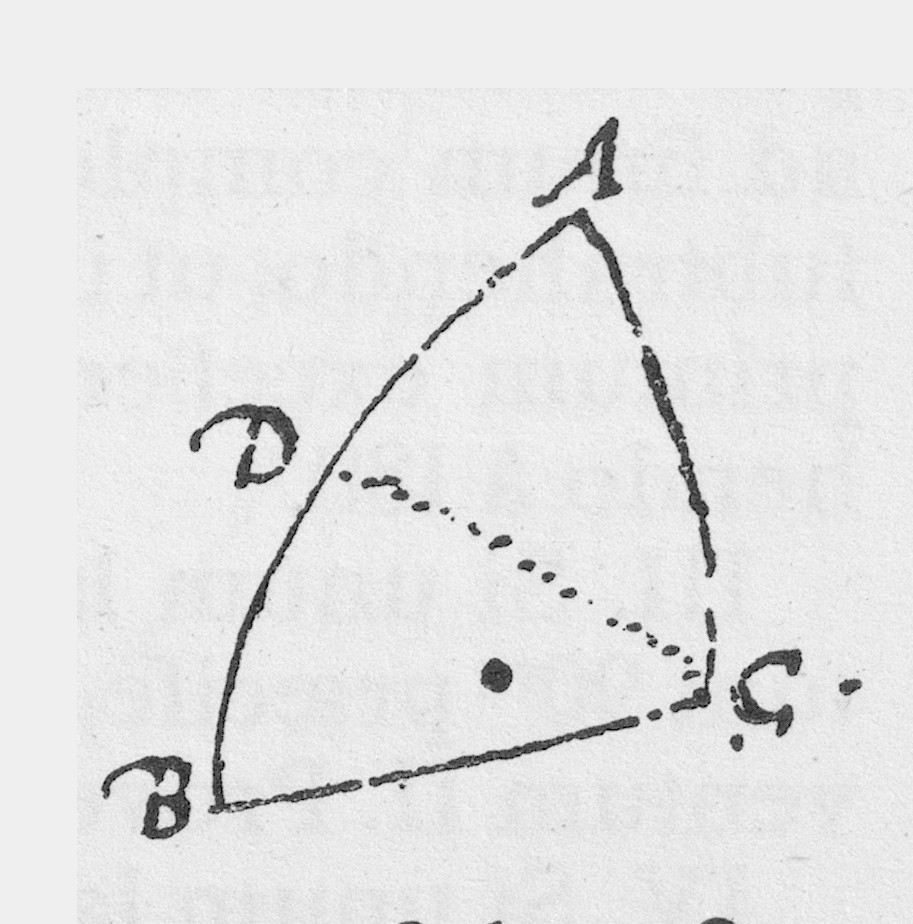
I. Operatio] Minus datum, et complementum maioris invicem adde, et aufer, utriusque residui sinus invicem subtractos dimidia, et habebis sinum complementi lateris AD.
II. Deinde per I inquire DC.
|III. Demum in altero Triangulo Rectangulo BDC pro latere BC opposito Angulo recto, multiplica sinum lateris DC per totum, et divide per sinum Anguli dati ad B: exit sinus lateris BC.
IV. Pro latere BD operare per I, et minus latus DC, et supplementum maioris BC, invicem adde, et aufer; sinus utriusque adde, et dimidia; habesque sinum complementi lateris DB, ideoque ipsum BD.
Latus itaque DB adde ad AD prius inventum, et habebis totum BA cognitum. Pro angulo vero ACB per III, ut supra, inquire Angulum DCB, quem adde angulo ACD prius invento, et constabit totus Angulus ACB, qui quærebatur. Similis est operatio, cum cadit perpendicularis extra Triangulum.
|DOGMA IX SPHÆRICORUM.
Trianguli non Rectanguli, datis tribus lateribus, Angulum quemvis invenire.
|Duorum laterum, angulum quæsitum ambientium, minus latus, et supplementum maioris invicem adde, et aufer, ac utriusque residui sinus adde, si supplementum maioris lateris excedit latus minus; alias aufer; producti dimidium est inventum I, quod ablatum ab aggregato primo dat inventum II. Tertium inventum est differentia inventi primi et sinus complementi lateris reliqui oppositi Angulo quæsito. Deinde multiplica inventum III per totum, et divide per inventum II. Exit sinus complementi Anguli quæsiti, si acutus fuerit; sin obtusus, Arcus inventus ipsius Anguli adiungendus est Quadranti (Est autem hic angulus acutus, quando inventum I minus est sinu complementi lateris tertij oppositi, obtusus vero, quando eodem maius est).
CASUS VARIJ.
I. N. Si latera ambientia 90 excesserint, sume complementum |â polo Australi.
II. Quando vero maius latus excesserit Quadrantem, operandum est per excessum eius de 90, et habebis inventum III, addendo inventum I ad sinum complementi lateris subtendentis Angulum quæsitum, non subtrahendo, ut in Dogmate extat; alias iuxta Dogma. Et si aggregatum primum excesserit quadrantem, habebis aggregatum verum, subtrahendo â 180.
III. Si unum laterum ambientium 90ta excesserit, latus vero oppositum 90ta præcise, adde invento primo integrum sinum, et divide per inventum II. Provenit complementum Anguli quæsiti. Aliter:
IV. Si unum laterum ambientium quæsitum Angulum cum opposito eidem excedat Quadrantem oppositi, subtrahendo inventum I ab huius sinu.