||DE TRIANGULIS PLANIS COMPENDIUM CONTINENS DOGMATA SEPTEM.
|DOGMA I PLANORUM.
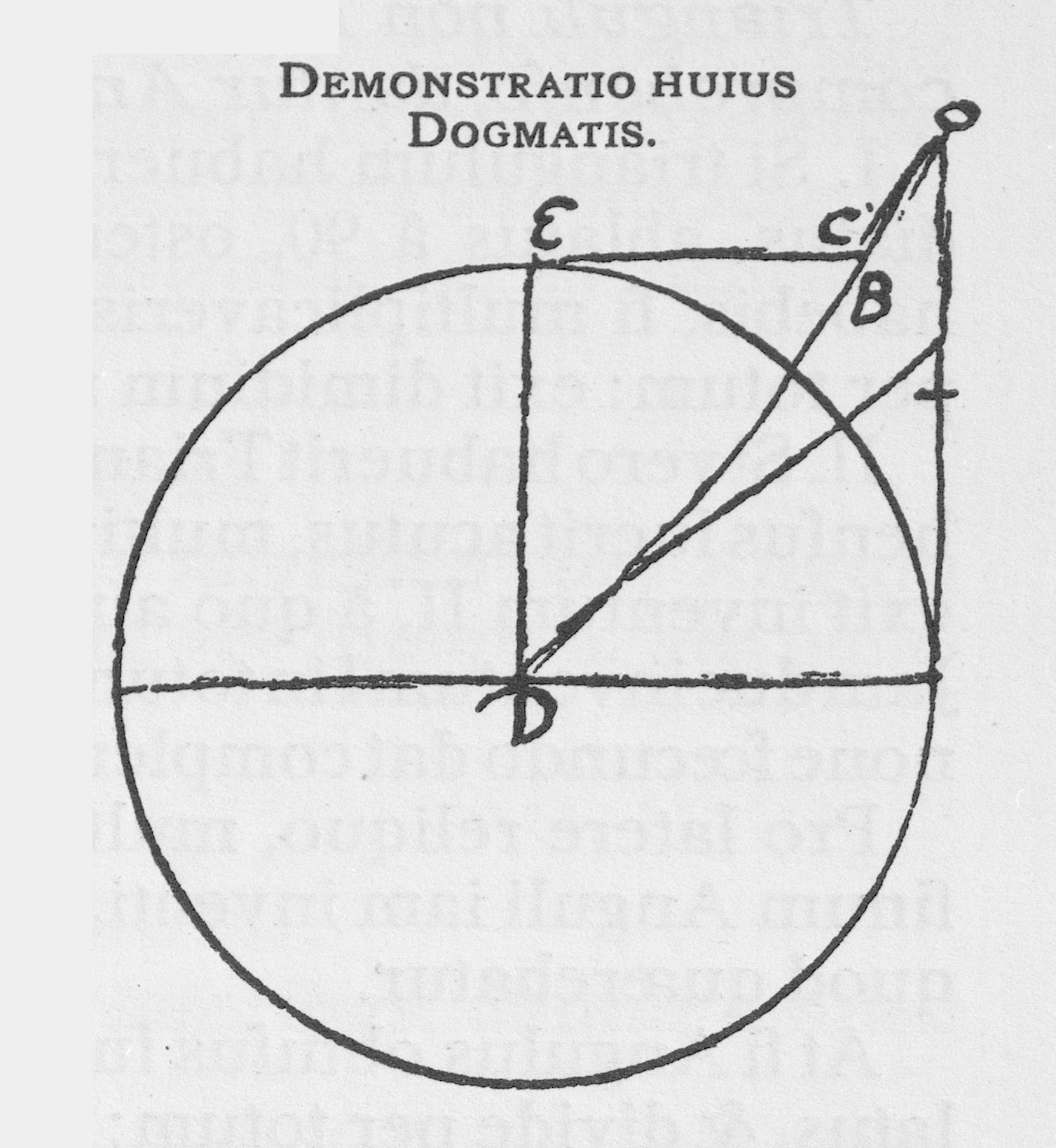
Trianguli Rectanguli, datis duobus lateribus circa rectum, datur uterque Angulorum cum Latere reliquo.
Pro Angulis] Multiplica latus oppositum Angulo quæsito per totum, et productum divide per latus reliquum: exit numerus, qui in areâ Canonis fœcundi quæsitus, angulum quæsitum ostendet; Reliquum Angulum dat huius complementum ad 90.
Pro latere] Quod recto subtenditur, multiplica alterum latus per totum, et divide in sinum Anguli, cui idem latus subtenditur: exit ipsum latus quæsitum, quod Angulo Recto opponitur.
|DOGMA II PLANORUM.
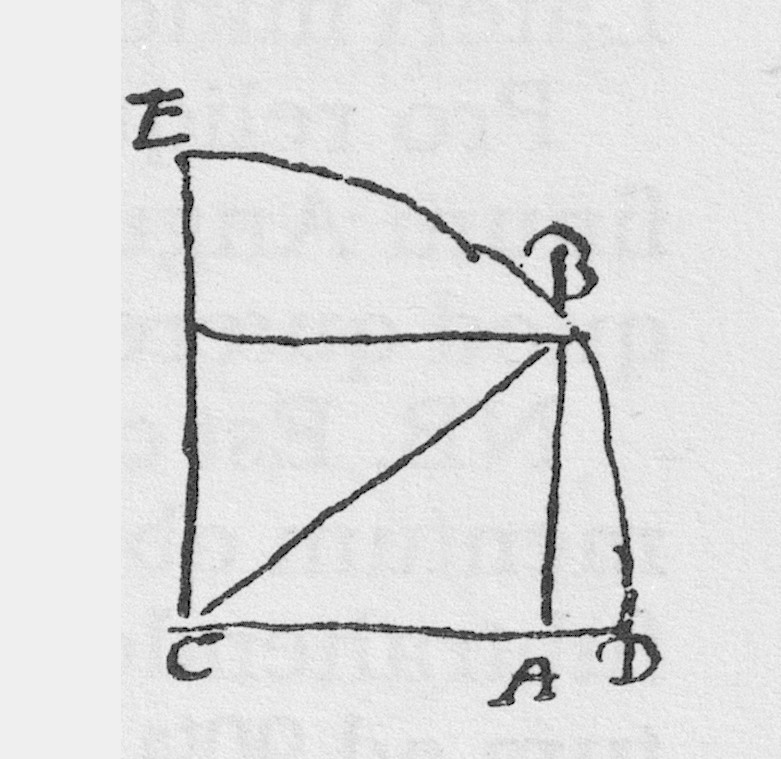
Trianguli Rectanguli, datis duobus lateribus, quorum alterum circa rectum, alterum eidem opponitur, dantur Anguli, et reliquum latus.
Latus circa Rectum multiplica per totum, et divide per latus recto subtensum: exit sinus Anguli, cui latus illud subtenditur, cuius arcus complementum ad 90 dat tertium Angulum. Huius sinum si multiplicaveris per latus recto subtensum, et diviseris per totum, exit alterum latus circa rectum, quod quærebatur.
|DOGMA III PLANORUM.
Trianguli Rectanguli, dato altero acutorum cum uno latere, dantur reliqua duo latera.
I. Si latus Rectum subtendens Angulum fuerit datum, multiplica mensuram eius lateris per sinum Anguli, cui opponitur latus quæsitum, et divide per totum: exit latus, quod quærebatur.
II. Si vero alterum duorum laterum recto adiacentium detur, et volueris mensurare latus Rectum subtendens Angulum, multiplica latus datum per totum, et divide per sinum Anguli sibi oppositi: exit mensura lateris Recto oppositi.
|III. Si reliquum latus Recto adiacens voles inquirere, numerum lateris dati per sinum complementi Anguli sibi oppositi multiplica, et divide per eiusdem Anguli sinum: exit latus reliquum, quod quærebatur.
|DOGMA IV PLANORUM.
Trianguli non Rectanguli, datis duobus lateribus cum Angulo comprehenso, dantur Anguli, et reliquum latus.
I. Si triangulum habuerit duo æqualia latera, Angulus datus dimidiatus, ablatus â 90, ostendit reliquos Angulos; Latus vero tertium habebis, si multiplicaveris latus per dimidium Anguli dati, et dividas per totum: exit dimidium reliqui lateris, quod duplica.
II.Si vero habuerit Triangulum inæqualia latera, et Angulus comprehensus fuerit acutus, multiplica maius latus datum, et divide per totum: exit inventum II, â quo aufer minus latus, et relinquitur inventum III. Jam duc inventum I in totum, et divide per inventum III: productum in Canone fœcundo dat complementum Anguli, qui lateri maiori opponitur.
Pro latere reliquo, multiplica inventum I per |totum, et divide per sinum Anguli iam inventi, oppositi lateri maiori: exit latus reliquum, quod quærebatur.
At si Angulus obtusus fuerit, duc sinum complementi obtusi in maius latus, et divide per totum: exit inventum I. Deinde duc sinum obtusi in maius Latus, et divide per totum: exit inventum II. Postea adde I inventum dato minori lateri, et habebis inventum III. Jam duc inventum II in totum, et divide per inventum III: exit numerus Anguli, qui adiacet Lateri minori, in Tabulâ fœcundâ inquirendi.
Pro reliquo latere multiplica inventum II per totum, et divide per sinum Anguli modo inventi, qui adiacet Lateri minori: exit latus III, quod quærebatur.
NB. Est complementum ad 180, ubi Angulus is est obtusus. Complementum obtusi habes, subtrahendo ab eo 90. Sinum vero obtusi habes subtrahendo eum a 180, et residui sinum accipiendo, prioris complementum ad 90ta.
| COMPENDIOSIOR SOLUTIO HUIUS DOGMATIS ABSQUE DEMISSA PERPENDICULARI.
I. Dati Anguli (acuti vel obtusi) complementum a semicirculo, id est 180, dimidia, et huius tangentem ex Canone Tangentium accipe.
II. Deinde adde minus latus datum lateri maiori dato, et aggregatum dimidia, quod erit inventum I.
III. Ab hoc invento primo subtrahe minus latus denuo, et residuum erit inventum II.
IV. Tertium autem inventum erit Tangens Anguli, ex complemento dati Anguli prius dimidiato.
|Πρᾶξις.
Duc iam inventum II in inventum III, et divide per inventum I: exit Tangens Anguli differentiæ Angulorum, quibus data latera subtendebantur. Itaque si hanc differentiam in Canone Tangentium inventam subtraxeris ab Angulo prius per complementum dimidiatum invento, pa|tescet Angulus, cui minus datorum laterum subtendebatur. Hanc rursus si addideris eidem Angulo ex complemento invento, manifestatur angulus â maiori latere subtenso. Vel etiam, datis duobus Angulis in Triangulis planis, tertius per eorum complementum ad semicirculum notus existit.
DOGMA V PLANORUM.
Datis Trianguli non Rectanguli duobus lateribus cum Angulo opposito, vel duobus Angulis cum Latere, vel subtenso, vel adiacente, reliqua hinc invenire.|
.....................................
|DOGMA VI PLANORUM.
Trianguli non Rectanguli, datis tribus lateribus, dantur omnes Anguli.
I. ISOPLEURUM. In Triangulo trium Æqualium laterum, quod ISOPLEURUM vocant, Anguli 60 partes obtinent.
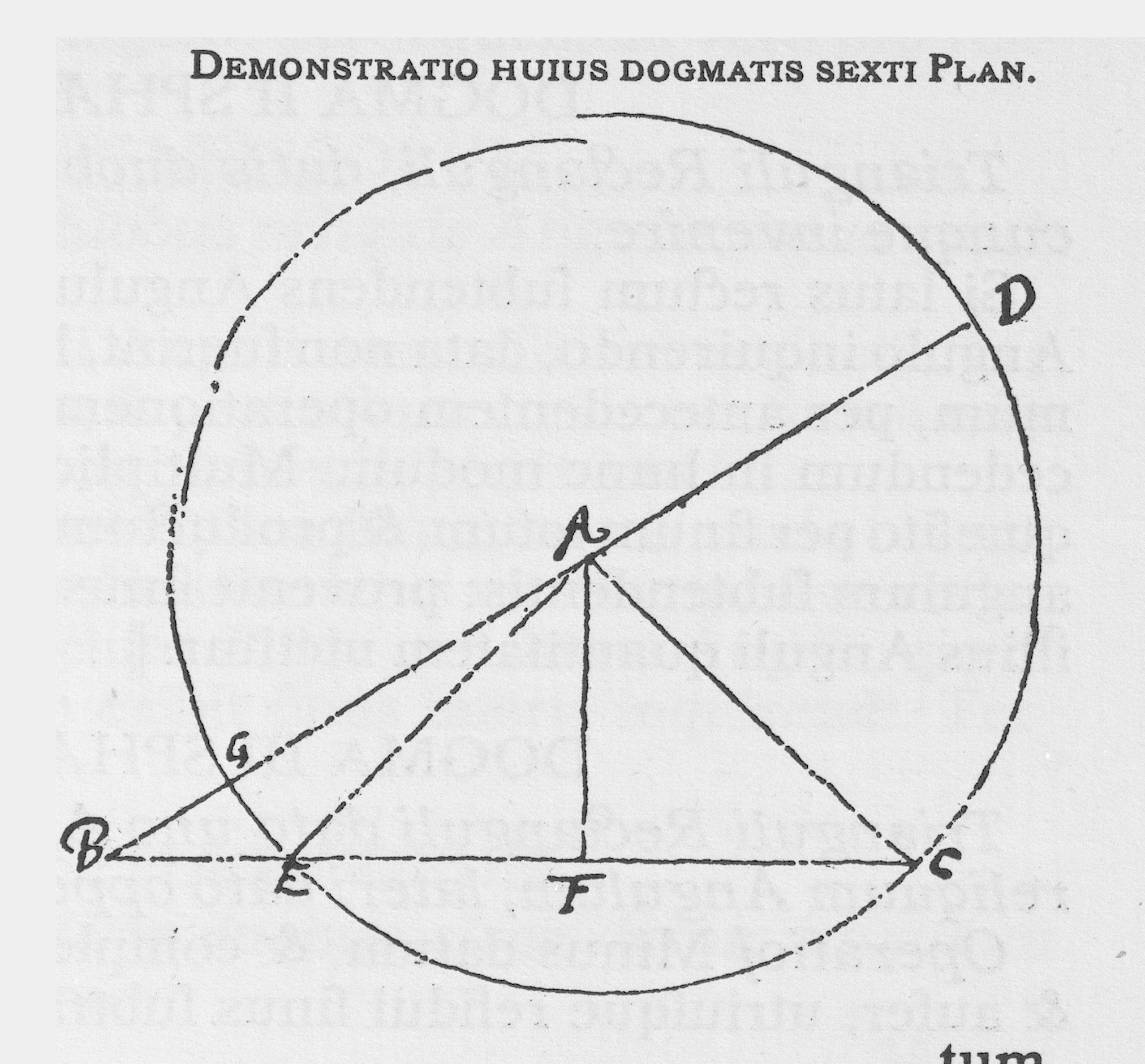
II. ÆQUICRURIUM. In Triangulo duorum æqualium laterum, quod ÆQUICRURIUM vocant, dimidiam basin multiplica per totum, et divide per alterum æqualium laterum: exit sinus Anguli dimidij, â duobus æqualibus lateribus comprehensi. Quare, cum reliqui sint æquales, huius complementum ad 180, dimidiatam utriusque reliqui Anguli quantitatem indicabit.
II. SCALENUM. In Triangulo trium inæqualium laterum: accipe latus minus, et proxime maius, illa adde invicem, et subtrahe, ambo residua invicem multiplica, et productum divide per maximum latus: habes inventum I. Hoc ab eodem maximo latere aufer, et residuum dimidia, idque invento I adde, et habe|bis inventum II. Hoc inventum secundum multiplica per to|tum, et divide per latus medium, scilicet proxime maius minimo: exit sinus complementi Anguli, qui minimo lateri opponitur. Pro reliquo Angulo, accipe residui dimidium prius datum (per inventum semicompletum secundum) et latus minimum, tanquam oppositum Angulo (quod subintelligitur) recto, et per secundam huius dabitur Angulus oppositus lateri mediocri, ergo et tertius notus erit.
|DOGMA VII PLANORUM.
Trianguli, tribus cognitis Angulis, latera singula invenire.
Anguli cuiusvis sinum duplica, et proveniet quantitas lateris oppositi huic Angulo, in talibus partibus, qualium semidiameter Circuli est sinus totus.
